Question

Can you help with a compound equality

Answer 1

Compounding inequalities

In general, a compound inequality consists of two inequalities joined by the word "and" or the word "or". Let's focus on the "or" case:

Example.

We aim to find a set of numbers satisfying at least one of the equations. The idea is to solve each equation independently as you showed me:

We've obtained two simplified inequalities. The next step is to understand each of them as sets and join them by a union of sets ("capital u"). Let's begin with the inequality on the left. It represents all numbers "dominated" by 2 and 2 is not included (for it's strict). Then, in terms of sets, it looks like

`(-\infty,2)\text{.}`

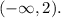
The right parenthesis means that 2 is not included, and "minus infinite" expresses the idea of all numbers below.

Let's analyze the second inequality. In this case, we aren't interested in the numbers below but the numbers above 2, where 2 is included. In terms of sets, it looks like

`\lbrack2,\infty)\text{.}`

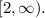
The bracket means that 2 is included. The infinite on the right captures the idea of "all numbers above". The answer to the compound inequality is the union of both sets:

`(-\infty,2)\cup\lbrack2,\infty)\text{.}`

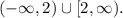
Surprisingly, the solution is all numbers!