Given:
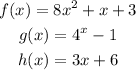
a) the average rate of change in the interval [3,5] is,
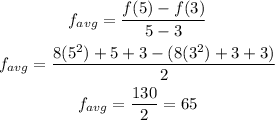
Also,
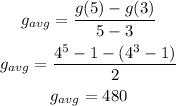
And,

Option a) is not correct. because the average rate of change of g and h is not more than f.
b) for the interval [0,2],
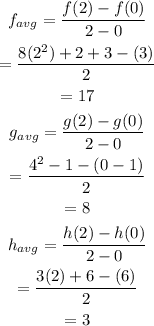
Option b) is also not correct.
when x approaches to infinity, the values of g(x) and h(x) exceeds the values of f(x).
Answer: option d)