Question

Rewrite the quadratic function f(x)=x^2-3x+2 into standard form. Identify its vertex and all its intercepts.

Answer 1

Given

`f\mleft(x\mright)=x^2-3x+2`

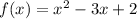
Find

Rewrite it into standard form and identify vertex and all its intercepts.

Step-by-step explanation

standard form =

`f(x)=a(x-h)^2+k`

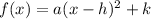
where (h , k) be the vertex

so ,

`\begin{gathered} f(x)=x^2-3x+2 \\ x^2-3x+(9)/(4)=-2+(9)/(4) \\ (x-(3)/(2))^2=(1)/(4) \\ f(x)=(x-(3)/(2))^2-(1)/(4) \\ \end{gathered}`

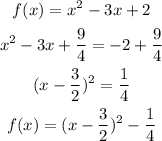
so vertex be

`((3)/(2),-(1)/(4))`

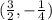
for intercept put f(x) = 0

`\begin{gathered} x^2-3x+2=0 \\ (x-1)(x-2)=0 \\ x=1,2 \end{gathered}`

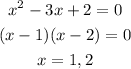
so , x - intercept = (1 , 0) and (2 , 0)

for y- intercept put x =0

`\begin{gathered} y=(0)^2-3(0)+2 \\ y=2 \end{gathered}`

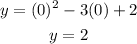
y - intercept (0 , 2)

Final Answer

Therefore , vertex is (3/2,-1/4)

x - intercept = (1 , 0) and (2 , 0) and y - intercept (0 , 2)