Question

In 1960, there were 244,775 immigrants admitted to a country. In 2009, the number was 1,066,824.a. Assuming that the change in immigration is linear, write an equation expressing the number of immigrants, y, in terms of t, the number of years after 1900.b. Use your result in part a to predict the number of immigrants admitted to the country in 2017.c. Considering the value of the y-intercept in your answer to part a, discuss the validity of using this equation to model the number of immigrants throughout the entire 20th century.Answers:a. A linear equation for the number of immigrants is y=.(Type your answer in slope-intercept form. Use integers or decimals for any numbers in the equation. Type an integer or decimal rounded to two decimal places asneeded.)b. The number of immigrants admitted to the country in 2017 will be approximately.(Round to the nearest whole number as needed.)c. Choose the correct answer below.A. The actual model may or may not be linear. More data points would help model the data more accurately. Using just two data points to create a linear model is not valid.B. The y-intercept gives the number of immigrants in 1900. The equation in part a is valid to model the number of immigrants throughout the entire 20th century.

Answer 1

a) We have to write an equation (linear model) to represent the immigration.

The dependent variable (y) is the number of immigrants while the independent variable (t) is the number of years after 1900

We have two data points:

- In 1960 the number of immigrants was 244775. This can be represented with the point (60, 244775).

- In 2009 the number of immigrants was 1066824. This can be represented with the point (109, 1066824).

We can calculate the slope of the line (m) using these two points as:

`\begin{gathered} m=(y_2-y_1)/(t_2-t_1) \\ \\ m=(1066824-244775)/(109-60) \\ \\ m=(822049)/(49) \\ \\ m=16776.51 \end{gathered}`

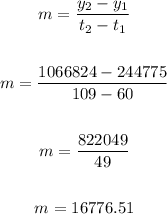
We can then use one of the points, like (60, 244775) and the slope to write the equation in slope-point form and then rearrange the equation:

`\begin{gathered} y-y_0=m(t-t_0) \\ y-244775=16776.51(t-60) \\ y-244775=16776.51\cdot t-1006590.61 \\ y=16776.51\cdot t-1006590.61+244775 \\ y=16776.51\cdot t-761815.61 \end{gathered}`

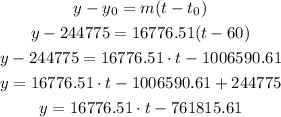
We can check this result with a graph as:

b) We now have to find what the model predicts for 2017.

As t is measured as years after 1900,the year 2017 corresponds to t = 117.

We then use the linear model to calculate the number of inmigrants:

`\begin{gathered} y=16776.51(117)-761815.61 \\ y=1962851.67-761815.61 \\ y\approx1201036 \end{gathered}`

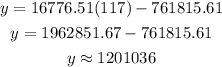
The predicted number is 1,201,036 immigrants in 2017.

c) This model can not be accurate for the years across the 20th century. For example, we can see that the model predicts negative values for t around 40 or less.

That is not accurate.

The model should be based on more data and probably corresponds to an exponential or another non-linear model.

Answer:

a) A linear equation for the number of immigrants is y = 16,776.51t - 761,815.61

b) The number of immigrants admitted to the country in 2017 will be approximately 1,201,036.

c) Correct Answer:

A. The actual model may or may not be linear. More data points would help model the data more accurately. Using just two data points to create a linear model is not valid.