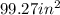Question

theres a semicircle and a triangle i need to find the area of both figures. The triangle has a height of 10". Semicircle has the base of 12".

Answer 1

Assuming that the figure resembles the following diagram:

Then, notice that we can find the area of the triangle and the area of the semicircle and then add them to find the total area of the figure.

The area of the triangle is given by:

`A=(1)/(2)bh`

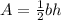
Where b is the base of the triangle and h is the height of the triangle. In this case, b=10in and h=12in, then:

`\begin{gathered} A=(1)/(2)(10in)(12in) \\ =(1)/(2)(120in^2) \\ =60in^2 \end{gathered}`

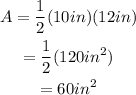
The area of a semicircle is half the area of a circle:

`A=(1)/(2)\pi r^2`

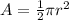
Since the radius of a circle is half its diameter, then r=5in. Then, the area of the semicircle is:

`\begin{gathered} A=(1)/(2)\pi(5in)^2 \\ =(25)/(2)\pi in^2 \\ \approx39.27\text{ in} \end{gathered}`

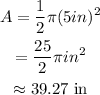
Add the area of both figures to find the total area of the given shape:

`A=60in^2+39.27in^2=99.27in^2`

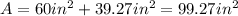
Therefore, the total area of the figure is approximately:

`99.27in^2`