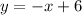The equation of the line in slope-intercept form is,
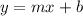
where,
m = slope
The equation of the line given is,
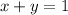
Let us now rearrange the equation in the slope-intercept form in order to obtain the slope.
Therefore,
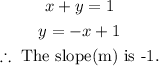
We were told the point is parallel to the equation of the line.
The rule for parallelism is,
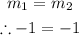
The formula to calculate for the equation of a line given one point is,

Given
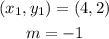
Substitute and simplify
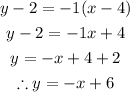
Hence, the equation of the line in slope-intercept form is