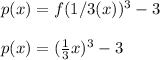Question

Describe how the formula is a transformation of a toolkit function. Then sketch a graph of the transformation.. Be sure to include labels for the increments on your x and y axis. Take a picture of that written work and upload it when submitting your answer. You may want to create a table of values to help you graph the function.p(x)=(\frac {1}{3}x)^3-3

Answer 1

The graph of the toolkit function was horizontally compressed by a factor of 1/3 and vertically shifted down 3 units to produce a graph of the transformed function.

In Mathematics and Geometry, a function can be compressed by multiplying it with a numerical value that is less than 1. This ultimately implies that, the graph of a function is either stretched or compressed when the factor (a) is less than zero (0);

0 < a < 1

Based on the information provided above, we can reasonably infer and logically deduce that the toolkit function represents the parent cubic function and it can be modeled by this equation;

`f(x) = x^3`

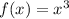
In this context, the graph of the parent cubic function was horizontally compressed by a factor of 1/3 and vertically shifted down 3 units, in order to produce a graph of the transformed cubic function;

`p(x) = f(1/3(x))^3 - 3\\\\p(x)=(\frac {1}{3}x)^3-3`

Answer 2

Given the function:

`p(x)=((1)/(3)x)^3-3`

The parent function to the given function is f(x) = x³

To get the function p(x) from f(x), we will perform the following translations:

1) Horizontal stretch with a factor of 1/3

2) Shift downward 3 units

The graph of f(x) and p(x) will be as shown in the following picture: