Question

8. Pentagon MNOPQ with M(-4,1),N(-2,3). O(0, 3), P(4, 3), and Q(2,-7): rotate 90° counterclockwise, then dilate by a factor of 2/3 120 What are the two arrow rules to show this composition? 12 b. Is the dilation an enlargement or reduction? How do you know? 710 с. What are the vertices of the image after the transformation?

Answer 1

Given data:

The given coordinates of the pentagon are M(-4,1),N(-2,3). O(0, 3), P(4, 3), and Q(2,-7).

The coordinatte after 90 degrees counterclockwise rotation is,

`\begin{gathered} M(-4,1)\rightarrow M^(\prime)(-1,\text{ -4)} \\ N(-2,\text{ 3)}\rightarrow N^(\prime)(-3,\text{ -2)} \\ O(0,\text{ 3)}\rightarrow O^(\prime)(-3,\text{ 0)} \\ P(4,\text{ 3)}\rightarrow P^(\prime)(-3,\text{ 4)} \\ Q(2,\text{ -7)}\rightarrow Q^(\prime)(7,\text{ 2)} \end{gathered}`

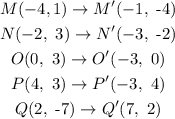
The final coordinates after 2/3 dilation factor is,

`\begin{gathered} M^(\doubleprime)\rightarrow(2)/(3)(-1,\text{ -4)} \\ \rightarrow(-(2)/(3),\text{ - }(8)/(3)) \\ N^(\prime\prime)\rightarrow(2)/(3)(-3,\text{ -2)} \\ \rightarrow(-2,\text{ -}(4)/(3)) \\ O^(\doubleprime)\rightarrow(2)/(3)(-3,\text{ 0)} \\ \rightarrow(-2,\text{ 0)} \\ P^(\doubleprime)\rightarrow(2)/(3)(-3,\text{ 4)} \\ \rightarrow(-2,(8)/(3))^{} \\ Q^(\doubleprime)\rightarrow(2)/(3)(7,\text{ 2)} \\ \rightarrow((14)/(3),\text{ }(4)/(3)) \end{gathered}`

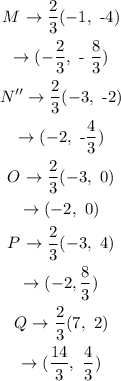
Thus, the final coordinates after transformation are M''(-2/3, -8/3), N''(-2, -4/3). O''(-2, 0), P''(-2, 8/3), and Q''(14/3, 4/3).