Question

Use a double-angle formula to rewrite the expression.7 − 14 sin2 x

Answer 1

The expression
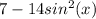`7-14sin^2(x)` can be rewritten using the double-angle formula as cos(2x).

The double-angle formula for sine is sin(2θ)=2sin(θ)cos(θ)

To rewrite
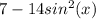`7-14sin^2 (x)` using the double-angle formula, we'll first express
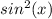`sin^2 (x)` in terms of the double-angle formula.

`sin^2 (x)`=
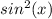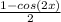`(1-cos(2x))/(2)`​ (using the identity
`sin^2 (x)`=
`(1-cos(2x))/(2)`

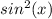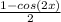
So,
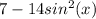`7-14sin^2(x)` becomes:

`7-14 * (1-cos(2x))/(2)`

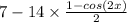
​Simplify that to get the expression in terms of cos(2x).

So, the expression
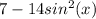`7-14sin^2(x)` can be rewritten using the double-angle formula as cos(2x).

Answer 2

`7\cos \left(2x\right)`

1) The point here is to use a double-angle formula, so let's pick this double-angle identity below:

`1-2\sin ^2\left(x\right)=\cos \left(2x\right)`

2) Now, let's rewrite that expression by making use of that expression above, and factoring it:

`\begin{gathered} 7-14\sin^2\left(x\right)\:\:\: \\ \\ 7\cdot \:1-7\cdot \:2\sin ^2\left(x\right) \\ \\ 7\left(1-2\sin ^2\left(x\right)\right) \\ \\ \left(1-2\sin^2\left(x\right)\right)7\:\:\:Use\:this\:double\:angle\:identity:\:1-2\sin^2\left(x\right)=\cos\left(2x\right) \\ \\ (\cos(2x))7 \\ \\ 7\cos \left(2x\right) \end{gathered}`

Note that we could simplify that since at the end, we could match it with the formula above.