For question a), we have to write the equation of the cost (c) as a function of the minutes (m), so:
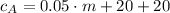
In the equation above the term 0.05*m represent the 5 cents for minute then we have to sum the $20 for 250 texts and $20 of service fee.
Before we draw the lines, we can solve the question c). If a customer wants to spend $75 monthly we can recommen him the plan wich more minutes for that cost, so we need to calculate the minutes for each plan:

The customer should choose the Plan A, because it has more minutes and more texts for $75.
For point b), we can evaluate each equation in two differents m-values and found the pairs (m, c) to graph the lines, so:

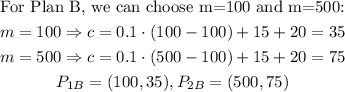
And the graphs are:
In the Graphs we can see the lines intercept in m=300 and evluating the equations in that value the cost is $55.