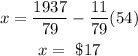Question

For a project in statistics class, a pair of students decided to invest in two companies, one that produces software and one that does biotechnology research. Kendall purchased 86 shares in the software company and 11 shares in the biotech firm, which cost a total of $2,056. At the same time, Audrey invested a total of $1,937 in 79 shares in the software company and 11 shares in the biotech firm. How much did each share cost?Each share in the software company cost $? and each share in the biotech firm cost $?

Answer 1

`\begin{gathered} \text{ Each share in the software company cost \$17.} \\ \text{ Each share in the biotech firm cost \$54.} \end{gathered}`

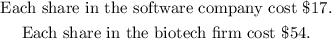
Explanation:

Use a system of linear equations to solve the situation. If Kendall purchased 86 shares in the software company and 11 shares in the biotech firm, which cost a total of $2,056.

`86x+11y=2056`

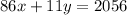
At the same time, Audrey invested a total of $1,937 in 79 shares in the software company and 11 shares in the biotech firm.

`79x+11y=1937`

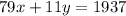
Let x be the cost of each share in the software company cost.

Let y be the cost of each share in the biotech firm cost.

Solve using the substitution method, isolate one of the variables on one of the equations and plug it into the other equation;

`\begin{gathered} x=(1937)/(79)-(11)/(79)y \\ Plug\text{ it into the first one:} \\ 86((1937)/(79)-(11)/(79)y)+11y=2056 \\ (166582)/(79)-(946)/(79)y+11y=2056 \\ -(77)/(79)y=-(4158)/(79) \\ y=(4158*79)/(77*79) \\ y=\text{ \$54} \end{gathered}`

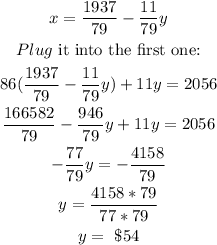
Then, the cost of a share in the biotech firm cost $54. Substitute into the isolated ''x'' equation, and solve for x.

`\begin{gathered} x=(1937)/(79)-(11)/(79)(54) \\ x=\text{ \$17} \end{gathered}`