1 Answer

Alscu · Answer 1 · 2023-03-15T22:12:21+0000

Hello!

Let's solve these questions to find the corresponding values.

First box:

$\begin{cases}y+12=x^2+x\text{ equation I} \\ x+y=\text{ }{3\text{ equation II}}\end{cases}$

Let's rewrite equation II (I'll just change the side of the values and their signal, to isolate one variable).

$\begin{gathered} x+y=3\rightarrow\boxed{y=3-x} \\ \end{gathered}$

Now, where's Y, we will replace it with (3 -x) in the second equation.

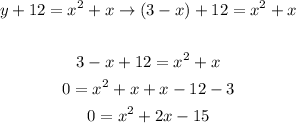
$\begin{gathered} y+12=x^2+x\rightarrow(3-x)+12=x^2+x \\ \\ 3-x+12=x^(2)+x \\ 0=x^2+x+x-12-3 \\ 0=x^2+2x-15 \end{gathered}$

Solving it, we'll obtain two values for x:

• x', = -5

,

• x", = 3

Now, let's calculate y' and y" by replacement:

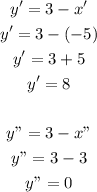
$\begin{gathered} y^(\prime)=3-x^(\prime) \\ y^(\prime)=3-(-5) \\ y^(\prime)=3+5 \\ y^(\prime)=8 \\ \\ y$

So, the solution for the first box is:

{ {-5, 8}; {3, 0} }

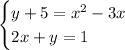
$\begin{cases}y+5={x^2-3x} \\ 2x+y={1}\end{cases}$

Let's solve it in a similar way:

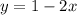
So, we have:

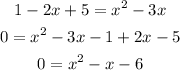
$\begin{gathered} 1-2x+5=x^2-3x \\ 0=x^2-3x-1+2x-5 \\ 0=x^2-x-6 \end{gathered}$

Solving it, we'll obtain two values for x:

• x', = -2

,

• x", = 3

Finding y' and y" by replacement, we have:

$\begin{gathered} y^(\prime)=1-2x\~ \\ y^(\prime)=1-2(-2) \\ y^(\prime)=1-(-4) \\ y^(\prime)=1+4 \\ y^(\prime)=5 \\ \\ y$

So, the solution for the third box is:

{ {-2, 5}; {3, -5} }