Question

Classifying parallelograms in the coordinate planePart B:Slope of KLSlope of side adjacent to KLPart c:From parts (a) and (b), what can we conclude about parallelogramJKLM? Check all that apply.O JKL M is a rectangle.O JKL M is a rhombus.O JKL M is a square.O JKL M is none of these

Answer 1

Given

J(2, -7) ; K(-6, -2) ; L(-1, 6) ; M(7, 1 )

Find

Length of KL and length of side adjacent to KL

Step-by-step explanation

by distance formula we find the length of sides.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

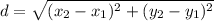
so ,

`\begin{gathered} JK=√((-6-2)^2+(-2+7)^2)=√(64+25)=√(89) \\ KL=√((-1+6)^2+(6+2)^2)=√(25+64)=√(89) \\ LM=√((7+1)^2+(1-6)^2)=√(25+64)=√(89) \\ MJ=√((7-2)^2+(1+7)^2)=√(25+64)=√(89) \\ JL=√((-1-2)^2+(6+7)^2)=√(9+169)=√(178) \\ KM=√((7+6)^2+(1+2)^2)=√(169+9)=√(178) \end{gathered}`

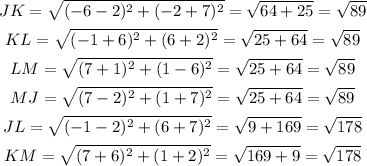
here all sides are equal and diagonal are equal , so it is a square .

a) Length of KL and length of side adjacent to KL is

`√(89)`

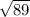
slope of KL is given by

`\begin{gathered} (y_2-y_1)/(x_2-x_1) \\ \\ (6+2)/(-1+6) \\ (8)/(5) \end{gathered}`

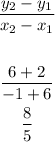
slope of side adjacent to KL is given by

`\begin{gathered} (1-6)/(7+1) \\ -(5)/(8) \end{gathered}`

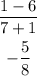
Final Answer

a) Length of KL and side adjacent to KL is

`√(89)`

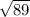
b) Slope of KL = 8/5

slope of side adjacent to KL is -5/8

c) it is a sqaure.