Question

The cost of a ticket to the circus is $15.00 for children and $37.00 for adults. On a certain day, attendance at the circus was 900 and the total gate revenue was $24,500. How many children and how many adults bought tickets?The number of children was (___) and the number of adult was (____).

Answer 1

Given:

The cost of a ticket to the circus is $15.00 for children and $37.00 for adults. On a certain day, attendance at the circus was 900 and the total gate revenue was $24,500.

Required:

We need to find that how many childern and adults were there

Step-by-step explanation:

Consider number of children as x and number of adults as y

so by attendance at the circus was 900 we can say that and call that equation as 1

`x+y=900`

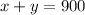
and by cost of a ticket to the circus is $15.00 for children and $37.00 for adults and total revenue was $24,500 we can say that and called that equation as 2

`15x+37y=24500`

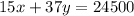
now multiply eq 1 with 15 and thn substract from eq 2

`\begin{gathered} 15x+37y-15x-15y=24500-13500 \\ 22y=11000 \\ y=500 \end{gathered}`

substitute the value of y in eq 1 to find the x

`\begin{gathered} x+500=900 \\ x=400 \end{gathered}`

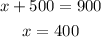
Final answer:

The number of children was 400 and the number of adult was 500