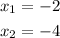Question

Convert the equation into vertex form, then solve the equation x^2 + 6x + 8 = 0

Answer 1

The Vertex form of a Quadratic function is:

`f(x)=a\mleft(x-h\mright)^2+k`

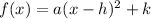
Where the vertex of the paraboola is:

`(h,k)`

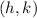
Given the following Quadratic equation:

`x^2+6x+8=0​`

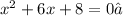
You need to convert it into Vertex form by completing the square. The steps are shown below:

- Identify the coefficient of the term with the variable "x". In this case, this is:

`b=6`

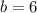
- Divide it by 2 and square it:

`((b)/(2))^2=((6)/(2))^2=3^2`

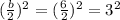
- Add and subtract the number obtained (in the right side of the equation):

`x^2+6x+8+3^2-3^2=0​`

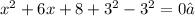
- Order it and express it as a square of a binomial, you get:

`\begin{gathered} (x^2+6x+3^2)+8-3^2=0​ \\ (x+3)^2-1=0 \end{gathered}`

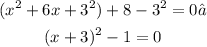
- Add 1 to both sides of the equation:

`\begin{gathered} (x+3)^2-1+1=0+1 \\ (x+3)^2=1 \end{gathered}`

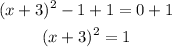
To solve the equation you must take the square root of both sides of the equation:

`\begin{gathered} \sqrt[]{(x+3)^2}=\pm\sqrt[]{1} \\ \\ x+3=\pm1 \end{gathered}`

Finally, subtract 3 from both sides of the equation:

`\begin{gathered} x+3-3=\pm1-3 \\ \\ x=-3\pm1 \\ \\ x_1=-3+1=-2 \\ x_2=-3-1=-4 \end{gathered}`

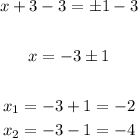
The answer is:

- Vertex form:

`(x+3)^2=1`

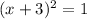
- Solutions:

`\begin{gathered} x_1=-2 \\ x_2=-4 \end{gathered}`