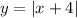According to the information given, each graph shows a translation of this Absolute Value Function:
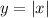
Then, you need to remember the following Transformation Rules for Functions:
1. If:
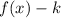
The function is translated down "k" units.
2. If:
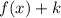
The function is translated up "k" units.
3. If:
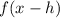
The function is translated right "h" units.
4. If:
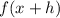
The function is translated left "h" units.
By definition, the Parent Function of an Absolute Value Parent Function is:
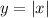
And its vertex is at the Origin.
Then, you can identify that:
a) The graph that is given in "Part a" shows that the Parent Function was translated down 3 units. Then, the new equation for the function is:

b) Notice that the graph that is given in "Part b", shows that the Parent Function was translated 1 unit up. Then, the new equation for the function is:
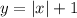
c) For this part, you can identify that the Parent Function was translated 1 unit to the right. So the equation is:
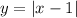
d) The graph shows that the Parent Function was translated 4 units to the left. Then, you can set up this equation:
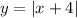
Therefore, the answers are:
a)

b)
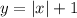
c)
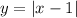
d)