Question

In Exercises 39 and 40, use the following information.A shot put is thrown a distance of 54.5 feet at a high school track and field meet.The shot put was released from a height of 6 feet and at an angle of 43°.39. Write a set of parametric equations for thepath of the shot put.Ans:x = (v*cos43°)t, y = -16t^2 + (v*sin43°)t + 6 -or-x = 0.731vt, y = -16t^2 + 0.682vt + 640. Use the equations to determine the speedof the shot put at the time of release.Must be solve without calc, but without t, how do you find v?I solved the quadratic and found t in terms of v, plugged that into the x-EQ, but it became a quartic, it’s an Alg 2 class so there must be a simpler solution …

Answer 1

We are asked to determine a set of parametric equations for the parabolic motion of an object. The parametric equations for such a motion is given by:

`\begin{gathered} x=v\cdot\cos 43\degree t,(1) \\ y=-16t^2+v\cdot\sin 43\degree t+6,(2) \end{gathered}`

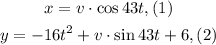
To determine the velocity we will solve for "t" in equation (1):

`t=(x)/(v\cos 43)`

Now, we will replace this in equation (2):

`y=-16((x)/(v\cos43))^2+v\cdot\sin 43\degree((x)/(v\cos43))+6`

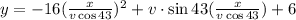
Simplifying:

`y=-(16x^2)/(v^2\cos^243)+x\tan 43+6`

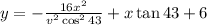
Now we replace the values x = 54.5 and y = 0:

`0=-(16(54.5)^2)/(v^2\cos^243)+(54.5)\tan 43+6`

Simplifying:

`0=-(88850.1)/(v^2)+56.82`

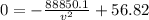
Now we solve for "v":

`(88850.1)/(v^2)=56.82`
`88850.1=56.82v^2`
`(88850.1)/(56.82)=v^2`

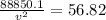
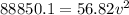
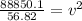
Solving the operation:

`1563.71=v^2`

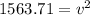
taking the square root:

`\begin{gathered} \sqrt[]{1563.71}=v \\ 39.54=v \end{gathered}`

Therefore, the velocity is 39.54 ft/s.