Question

Two airplanes leave an airport at the same time and travel in opposite directions. One plane travels 86 km slower than the other. If the two planes are 9450 h kilometers apart after 5 hours, what is the rate of each plane?

Answer 1

Let 'd' be the distance that the faster plane travels, then the distance that the slower plane travels is:

`9450-d`

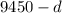
Now, let 's' be the speed of the faster plane, then similarly, the speed of the slower plane is:

`s-86`

We have the following equation for the faster plane:

`d=5\cdot s`

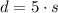
and the equation for the slower plane is:

`9450-d=5\cdot(s-86)`

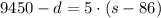
Now we can do the substitution d=5s on the second equation to find the value of s:

`\begin{gathered} d=5s \\ \Rightarrow9450-5s=5\cdot(s-86)=5s-430 \\ \Rightarrow9450+430=5s+5s=10s \\ \Rightarrow10s=9880 \\ \Rightarrow s=(9880)/(10)=988 \\ s=988 \end{gathered}`

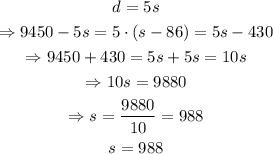
We have that the speed of the faster plane is s=988 km/h. Now we can find the speed of the slower plane:

`s-86=988-86=902`

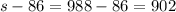
Finally, we can check the answer by finding the distance traveled:

`\begin{gathered} 9450-d=5\cdot(902) \\ \Rightarrow d=9450-5\cdot(902)=9450-4510=4940 \\ \text{and} \\ d=5(988)=4940 \end{gathered}`

Therefore, the speed of the faster plane is 988 km/h and the speed of the slower plane is 902 km/h