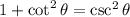Question

Use algebra to rewrite the following identity in 2 different forms. tan^2(θ) + 1 = sec^2(θ)

Answer 1

Let's rewrite the identity in two different forms conserving the functions given:

`\tan ^2\theta-\sec ^2\theta=-1`

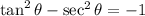
and

`\tan ^2\theta=\sec ^2\theta-1`

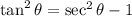
Now, let's find two different identities from this one. To do this let's remember that:

`\begin{gathered} \tan \theta=(\sin \theta)/(\cos \theta) \\ \sec \theta=(1)/(\cos \theta) \end{gathered}`

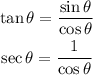
Then we have:

`\begin{gathered} \tan ^2\theta+1=\sec ^2\theta \\ \tan ^2\theta-\sec ^2\theta=-1 \\ (\sin^2\theta)/(\cos^2\theta)-(1)/(\cos^2\theta)=-1 \\ (\sin^2\theta-1)/(\cos^2\theta)=-1 \\ \sin ^2\theta-1=-\cos ^2\theta \\ \sin ^2\theta+\cos ^2\theta=1 \end{gathered}`

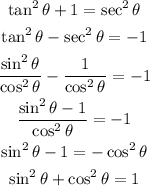
Therefore, we can write the identity given as:

`\sin ^2\theta+\cos ^2\theta=1`

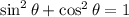
Let's find a second identity from the one given, to do this we will mutiply it by the cotangent squared of the angle:

`\begin{gathered} \tan ^2\theta+1=\sec ^2\theta \\ \tan ^2\theta\cdot\cot ^2\theta+\cot ^2\theta=\sec ^2\theta\cdot\cot ^2\theta \\ (\sin^2\theta)/(\cos^2\theta)\cdot(\cos^2\theta)/(\sin^2\theta)+\cot ^2\theta=(1)/(\cos^2\theta)\cdot(\cos ^2\theta)/(\sin ^2\theta) \\ 1+\cot ^2\theta=(1)/(\sin ^2\theta) \\ 1+\cot ^2\theta=\csc ^2\theta \end{gathered}`

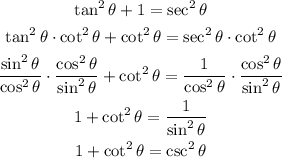
Therefore, we can write the identity given as:

`1+\cot ^2\theta=\csc ^2\theta`