Question

A coin is tossed, then aletter from the wordINDIANAPOLIS is selected atrandom. Find eachprobability.a) P(heads, then P)b) Pitails, then a vowel)c) P(tails, then N)d) P/heads, then D or I)

Answer 1

a) P(heads, then P) = (1/2) × (1/12) = (1/24) = 0.04167

b) P(tails, then a vowel) = (1/2) × (1/2) = (1/4) = 0.25

c) P(tails, then N) = (1/2) × (1/6) = (1/12) = 0.0833

d) P(heads, then D or I) = (1/2) × (1/3) = (1/6) = 0.1667

Step-by-step explanation

First of, we need to define what the probability of an event is

`\text{Probability of an event =}\frac{Number\text{ of elements in that event}}{Number\text{ of total elements in the sample space}}`

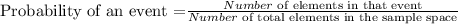
And when two independent events (two events whose probabilities do not depend on each other) happen one after the other, the total probability is the product of the two probabilities. That is, if A and B are independent events,

P (A n B) = P(A) × P(B)

So, we can start answering now,

a) P(heads, then P)

First of, we calculate the probability of a head turning up in a coin toss.

Probability of heads turning up in a coin toss = P(heads) = ?

Number of elements in the event = Number of heads possible in one coin toss = 1

Number of total elements in the sample space = Number of possible outcomes in a coin toss = 2 (It's usually either heads or tails!)

Probability of heads turning up in a coin toss = P(heads) = (1/2) = 0.5

Now, we calculate the probability of selecting a P from INDIANAPOLIS

Probability of selecting a P from INDIANAPOLIS = P (P) = ?

Number of elements in the event = Number of P's that are in INDIANAPOLIS = 1

Number of total elements in the sample space = Total number of letters in INDIANAPOLIS = 12

Probability of selecting a P from INDIANAPOLIS = P (P) = (1/12) = 0.08333

Now, we calculate the total probability of obtaining a head from the coin toss and then selecting P from INDIANAPOLIS

P(heads, then P) = (1/2) × (1/12) = (1/24) = 0.04167

b) P(tails, then a vowel)

First of, we calculate the probability of a tail turning up in a coin toss.

Probability of tails turning up in a coin toss = P(tails) = ?

Number of elements in the event = Number of heads possible in one coin toss = 1

Number of total elements in the sample space = Number of possible outcomes in a coin toss = 2 (It's usually either heads or tails!)

Probability of tails turning up in a coin toss = P(tails) = (1/2) = 0.5

Now, we calculate the probability of selecting a vowel from INDIANAPOLIS

Probability of selecting a vowel from INDIANAPOLIS = P (vowel) = ?

Number of elements in the event = Number of vowels that are in INDIANAPOLIS = 6

Number of total elements in the sample space = Total number of letters in INDIANAPOLIS = 12

Probability of selecting a vowel from INDIANAPOLIS = P(vowel) = (6/12) = (1/2) = 0.5

Now, we calculate the total probability of obtaining a tail from the coin toss and then selecting a vowel from INDIANAPOLIS

P(tails, then a vowel) = (1/2) × (1/2) = (1/4) = 0.25

c) P(tails, then N)

First of, we calculate the probability of a tail turning up in a coin toss.

Probability of tails turning up in a coin toss = P(tails) = ?

Number of elements in the event = Number of heads possible in one coin toss = 1

Number of total elements in the sample space = Number of possible outcomes in a coin toss = 2 (It's usually either heads or tails!)

Probability of tails turning up in a coin toss = P(tails) = (1/2) = 0.5

Now, we calculate the probability of selecting N from INDIANAPOLIS

Probability of selecting N from INDIANAPOLIS = P(N) = ?

Number of elements in the event = Number of N's that are in INDIANAPOLIS = 2

Number of total elements in the sample space = Total number of letters in INDIANAPOLIS = 12

Probability of selecting N from INDIANAPOLIS = P(N) = (2/12) = (1/6) = 0.1667

Now, we calculate the total probability of obtaining a tail from the coin toss and then selecting N from INDIANAPOLIS

P(tails, then N) = (1/2) × (1/6) = (1/12) = 0.0833

d) P(heads, then D or I)

First of, we calculate the probability of a head turning up in a coin toss.

Probability of heads turning up in a coin toss = P(heads) = ?

Number of elements in the event = Number of heads possible in one coin toss = 1

Number of total elements in the sample space = Number of possible outcomes in a coin toss = 2 (It's usually either heads or tails!)

Probability of heads turning up in a coin toss = P(heads) = (1/2) = 0.5

Now, we calculate the probability of selecting a D or I from INDIANAPOLIS

Probability of selecting a D or I from INDIANAPOLIS = P(D or I) = ?

Number of elements in the event = Number of D's or I's that are in INDIANAPOLIS = 4 (Three I's and one D)

Number of total elements in the sample space = Total number of letters in INDIANAPOLIS = 12

Probability of selecting a D or I from INDIANAPOLIS = P(D or I) = (4/12) = (1/3) = 0.3333

Now, we calculate the total probability of obtaining a head from the coin toss and then selecting D or I from INDIANAPOLIS

P(heads, then D or I) = (1/2) × (1/3) = (1/6) = 0.1667

Hope this Helps!!!