Question

Given r(x)=x3 - 4x2 +4x -6 find the value of r(2).

Answer 1

Given the function:

`r(x)=x^3-4x^2_{}+4x-6`

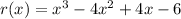
We are required to find the value of r(2).

This simply means we must substitute x = 2 wherever we see x in the function r(x).

This is done below:

`\begin{gathered} r(x)=x^3-4x^2+4x-6 \\ \text{substitute x = 2} \\ r(2)=2^3-4(2)^2+4(2)-6 \\ \\ \therefore r(2)=8-16+8-6 \\ r(2)=-6 \end{gathered}`

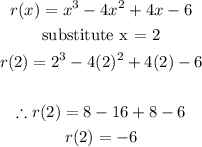
Therefore, r(2) = -6.

Step-by-step explanation:

Because when x = 2, r(2) = -6, it means that we can re-write x = 2 as:

`\begin{gathered} x=2 \\ \text{subtract 2 from both sides} \\ x-2=2-2 \\ x-2=0 \end{gathered}`

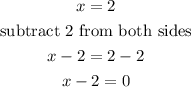
If r(2) were equal to zero i.e. r(2) = 0, it would have been a factor of r(x). But because

r(2) = -6, it means that (x - 2) divides r(x) and gives a remainder of -6.

Hence, (x-2) divides r(x) and leaves a remainder of -6