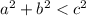Question

Suppose a triangle has sides a, b, and c, and the angle opposite the side of length b is obtuse. What must be true?

A. a^2 + c^2 < b^2
B. a^2 + c^2 > b^2
C. b^2 + c^2 < a^2
D. a^2 + b^2 < c^2

Answer 1

Answer: D.
`a^2 + b^2 < c^2`

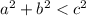
Explanation:

In the given figure, we have an obtuse triangle which has sides a, b, and c, and the angle opposite the side of length b is obtuse.

∵ In a triangle, the side opposite to the largest angle is largest.

Thus, the largest side in then given obtuse triangle= c

The Pythagorean inequalities theorem says that If a triangle is obtuse than the square of the largest side is greater than the sum of square of other two sides.

Therefore, we have

`a^2 + b^2 < c^2`