ANSWER
22.2 m
Step-by-step explanation
Let us make a sketch of the problem.
From the diagram:
T = top of the tower
B = Ball
O = Base of the tower
Now, we have to find x, which is the distance from the ball to the base of the tower.
Since the angle of depression is 42°, it means that angle
To find x, we can apply Pythagoras Rule:
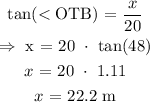
The distance of the ball from the base of the tower is 22.2 m