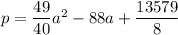Question

An insurance company charges a 35-year old non-smoker an annual premium of $118 for a $100,000 term life insurance policy. The premiums for 45-year olds and 55-year old no smokers are $218 and $563, respectively. Write a quadratic model for the premium p as a function of age a.

Answer 1

p=ma^2+ba+c, so you have 118=m35^2+35b+c 218=m45^2+45b+c 563=m55^2+55b+c so solving I get m=49/40 b=-88 c=13579/8 so its p=(49/40)a^2-88a+(13579/8)

Answer 2

`p=(49)/(40)a^2-88a+(13579)/(8)`

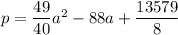
Explanation:

Let premium p for age of a , (p,a)

# An insurance company charges a 35-year old non-smoker an annual premium of $118 for a $100,000 term life insurance policy.

(35,118)

# An insurance company charges a 45-year old non-smoker an annual premium of $218 for a $100,000 term life insurance policy.

(45,218)

# An insurance company charges a 55-year old non-smoker an annual premium of $563 for a $100,000 term life insurance policy.

(55,563)

Let quadratic model be p=Aa²+Ba+C

Substitute the points into equation

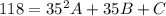
• For point, (35,118)

`118=35^2A+35B+C`

`118=1225A+35B+C` -------------(1)

• For point, (45,218)

`218=45^2A+45B+C`

`218=2025A+45B+C` -------------(2)

• For point, (55,563)

`563=55^2A+55B+C`

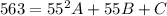
`563=3025A+55B+C` -------------(3)

Solve system of equation and find out A, B and C using calculator.

`A=(49)/(40),B=-88,C=(13579)/(8)`

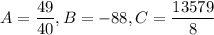
Quadratic model:

`p=(49)/(40)a^2-88a+(13579)/(8)`