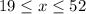Question

The U.S. senate is composed of 2 senators from each of the 50 states. In order for a treaty to be ratified, at least two thirds of the senators present must approve the treaty. Suppose all senators are present and 48 of them have voted in favor of a treaty. What are the possible numbers of additional senators who must vote in favor of the treaty in order to radify it?

Answer 1

Answer: So, the possible number of additional senators who must vote in favor of the treaty in order to radify it is given by

`19\leq x\leq 52`

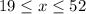
Explanation:

Since we have given that

Number of states = 50

Number of senators from each of the 50 states = 2

Total number of senators would be

`50* 2\\\\=100`

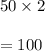
Since
`(2)/(3)` of the senators present must approve the treaty.

`(2)/(3)* 100\\\\=66.67`

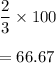
Number of senators have voted in favor of a treaty = 48

So, remaining senators would be

`67-48\\\\=19`

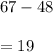
Let x be the number of senators needed.

So, Inequality would be

`x\geq 19`

Now,
`100-48=52`

`x\leq 52`

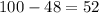
So, the possible number of additional senators who must vote in favor of the treaty in order to radify it is given by

`19\leq x\leq 52`

Answer 2

So there are 100 senators.
All are present.
You need at least 2/3 of the senators present.
So you need at least 66.66667
66 is not at least 66.66667, 67 is at least 66.66667.
So you need 67 total votes.
You already have 48.
Thus you need an additional 19.

I can't find any trick which would make the number 18.

The question asks for possible numbers which would ratify the treaty
so the answer should be 19, 20, 21, 22 and 52