Question

(Quadratic Regressions) Company X tried selling widgets at various prices to see how much profit they would make. The following table shows the widget selling price, x, and the total profitearned at that price, y. Write a quadratic regression equation for this set of data,rounding all coefficients to the nearest hundredth. Using this equation, find the profit, to the nearest dollar, for a selling price of 22 dollars.

Answer 1

The general quadratic equation is:

y = ax² + bx + c

where a, b and c are constants.

Substituting with x = 18.5 and y = 11397, we get:

11397 = a*18.5² + b*18.5 + c

11397 = 342.25a + 18.5b + c (eq. 1)

Substituting with x = 25.5 and y = 16256, we get:

16256 = a*25.5² + b*25.5 + c

16256 = 650.25a + 25.5b + c (eq. 2)

Substituting with x = 35 and y = 16109, we get:

16109 = a*35² + b*35 + c

16109 = 1225a + 35b + c (eq. 3)

Equations 1, 2 and 3 make a system of 3 equations and 3 variables (a, b, and c).

Isolating c from equation 1 and replacing into equations 2 and 3, we get:

11397 = 342.25a + 18.5b + c

11397 - 342.25a - 18.5b = c

16256 = 650.25a + 25.5b + 11397 - 342.25a - 18.5b

16256 - 11397 = 650.25a - 342.25a - 18.5b + 25.5b

4859 = 308a + 7b (eq. 4)

16109 = 1225a + 35b + 11397 - 342.25a - 18.5b

16109 - 11397 = 1225a - 342.25a - 18.5b + 35b

4712 = 882.75a + 16.5b (eq. 5)

Isolating b from equation 4 and replacing into equation 5, we get:

`\begin{gathered} 4859=308a+7b \\ 4859-308a=7b \\ (4859-308a)/(7)=b \end{gathered}`
`\begin{gathered} 4712=882.75a+16.5((4859-308a)/(7)) \\ 4712=882.75a+16.5\cdot(4859)/(7)-16.5\cdot(308)/(7)a \\ 4712=882.75a+11453.36-726a \\ 4712-11453.36=156.75a \\ -(6741.36)/(156.75)=a \\ -43=a \end{gathered}`

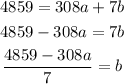
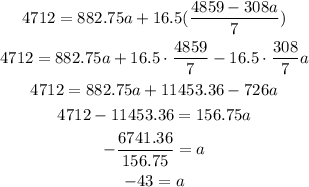
Then, the value of b is:

`\begin{gathered} b=(4859-308\cdot(-43))/(7) \\ b=(4859+13244)/(7) \\ b=(18103)/(7) \\ b=2586.14 \end{gathered}`

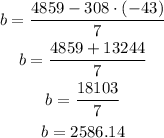
And the value of c is:

c = 11397 - 342.25*(-43) - 18.5*2586.14

c = 11397 + 14716.75 - 47843.59

c = -21729.84

Therefore, the quadratic regression is:

y = -43x² + 2586.14x - 21729.84

If the price is $22, then x = 22, and the value of y (profit) is:

y = -43*22² + 2586.14*22 - 21729.84

y = -20812 + 56895.08 - 21729.84

y = 14353.24