Question

If a person shoots a basketball overhand from a position of 8 feet from the floor, then the path of the basketball through the hoop can be modeled by the parabola y=(-16x^2/0.434v^2)+1.15x+8, where v is the velocity of the ball in ft/sec, y is the height of the hoop and x is the distance away from the hoop. If the basketball hoop is 10 feet high and located 17 feet away, what initial velocity v should the basketball have to go through the hoop?

Answer 1

The initial velocity of ball should be 0.0406 ft/s.

Explanation:

`y=(-16x^2)/(0.434v^2)+1.15x+8`

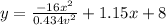
x = the distance away from the hoop

y = Height of the hoop

v = velocity of the ball

Given : x = 17 ft, y = 10 ft , v = ?

`10=(-16(17)^2)/(0.434v^2)+1.15* (17)+8`

`10-8-19.55=(-16(17)^2)/(0.434v^2)`

`(-17.55* 0.434)/(-16* (17)^2)=v^2`

`v^2=0.001647`

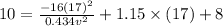
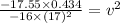
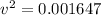
v = 0.0406 ft/s

The initial velocity of ball should be 0.0406 ft/s.