Step-by-step explanation
We must solve by two different methods the following equation:
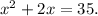
Method 1: Completing the square
1) We rewrite the equation above as:
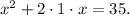
2) Now, we add 1² on both sides of the equation:
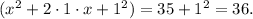
3) We see that the left and right sides can be written as squares:
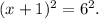
4) Taking the square root on both sides, we get two solutions:
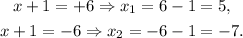
Method 2: Using the quadratic formula
1) We rewrite the equation above as:
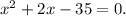
2) We identify a quadratic equation:

With coefficients:
• a = 1,
,
• b = 2,
,
• c = -35.
The roots of this equation are given by:
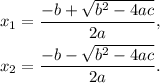
3) Replacing the coefficients of the quadratic equation in the formula above, we get:

Answer
The roots of the polynomial are:
• x₁ = 5
,
• x₂ = -7