Answer:
The radical form of the expression
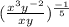 is
is
![\sqrt[5]{(y^3)/(x^2)}](https://img.qammunity.org/2016/formulas/mathematics/high-school/16adutkr46c92qq9882839kcnvmqe7x3s4.png)
Explanation:
Given :
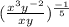
We have to simplify the given expression and write in radical form.
RADICAL FORM is the simplest form of expression that do not involve any negative exponent and power is less than n, where n is the nth root of that expression.
Consider the given expression
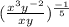
Cancel out the common factor x, we get,
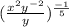
Using laws of exponents,
 , we have,
, we have,
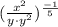
Using laws of exponents,
 , we have,
, we have,
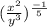
Again using laws of exponents,
 , we have,
, we have,
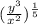
Also, written as
![\sqrt[5]{(y^3)/(x^2)}](https://img.qammunity.org/2016/formulas/mathematics/high-school/16adutkr46c92qq9882839kcnvmqe7x3s4.png)
Thus, the radical form of the expression
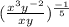 is
is
![\sqrt[5]{(y^3)/(x^2)}](https://img.qammunity.org/2016/formulas/mathematics/high-school/16adutkr46c92qq9882839kcnvmqe7x3s4.png)