Question

The number of bacteria in a refrigerated food product is given by N(T) = 27T^2 - 155T + 66, 6 < T < 36, where T is the temperature of the food.When the Food is removed from the refrigerator, the tempersture is given by T(t) = 6t + 1.7, where t is the time in hours.Find the composite function N(T(t)): N(T(t)) = 927t^2 - 379.2t - 119.47 (Already solved, don't need help with this question)Find the time when the bacteria count reaches 26087. Time needed = ____ hours(Not solved, need help!)

Answer 1

Given the functions:

`\begin{gathered} N(T)=27T^2-155T+66 \\ \\ T(t)=6t+1.7 \end{gathered}`

Where:

T is the temperature of the food.

t is the time in hours.

Let's solve for the following:

• (a). Find the composite N(T(t).

To find the composite function, we have:

N(T(t)) = N(6t + 1.7)

Substitute (6t+1.7) for T in N(T) and solve for N(6t + 1.7).

We have:

`\begin{gathered} N(6t+1.7)=27(6t+1.7)^2-155(6t+1.7)+66 \\ \\ =27(6t+1.7)(6t+1.7)-155(6t)-155(1.7)+66 \\ \\ =27(6t(6t+1.7)+1.7(6t_{}+1.7))-930t-263.5+66 \\ \\ =27(6t(6t)+6t(1.7)+1.7(6t)+1.7(1.7))-930t-197.5 \end{gathered}`

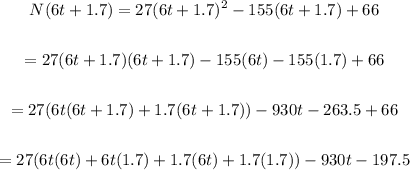
Solving further:

`\begin{gathered} =(27(36t^2)+27(20.4t)+27\cdot2.89)-930t-197.5 \\ \\ =972t^2+550.8t+78.03-930t-197.5 \\ \\ =972t^2+550.8t-930t+78.03-197.50 \\ \\ =972t^2-379.2t-119.47 \end{gathered}`

Therefore, the composite function is:

`N(T(t))=972t^2-379.2t-119.47`

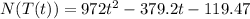
• (b). Find the time when the bacteria count reaches 26087.

Substitute 26087 for N(T(t)) and solve for t.

We have:

`26087=972t^2-379.2t-119.47`

Equate to zero.

Subtract 26087 from both sides:

`\begin{gathered} 972t^2-379.2t-119.47-260.87=26087-26087 \\ \\ 972t^2-379.2t-26206.47=0 \end{gathered}`

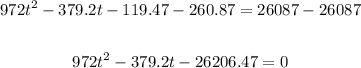
Solve using quadratic formula:

`t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Apply the standard quadratic formula to find the values of a, b, and c:

`\begin{gathered} ax^2+bx+c=0 \\ \\ 972t^2-379.2t-26206.47=0 \\ \\ \text{Factor out 0.03 from each term:} \\ 0.03(32400t^2-12640t-873549)=0 \\ \\ 32400t^2-12640t-873549=0 \end{gathered}`

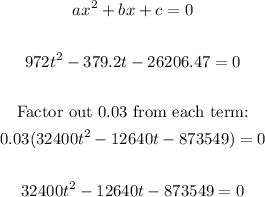
Thus, we have:

a = 32400

b = -12640

c = -873429

Input the values into the quadratic formula for solve for t:

`t=\frac{-(-12640)\pm\sqrt[]{113371720000_{}}}{2(32400)}`

Solving further:

`\begin{gathered} t=\frac{12640\pm200\sqrt[]{2834293}}{64800} \\ \\ t=\frac{316\pm5\sqrt[]{2834293}}{1620} \\ \\ t=\frac{316-5\sqrt[]{2834293}}{1620},\frac{316+5\sqrt[]{2834293}}{1620} \\ \\ t=-5.001,\text{ 5.}39 \end{gathered}`

We have the values:

t = -5.001

t = 5.39

Since the time cannot be negative, let's use the positive value.

Therefore, the time needed is 5.39 hours.

ANSWER:

5.39 hours.