Question

Suppose f(x) = x2. What is the graph of g(x) = f(2x)?10ухO A. *10n.B.1010уXO c.

Answer 1

The given information is:

f(x)=x^2

We need to find the graph of g(x)=f(2x).

We can make a table of values to find the graph of g(x).

As g(x)=f(2x) it means we need to replace the argument x in f(x) by 2x, so:

`\begin{gathered} g(x)=f(2x) \\ g(x)=(2x)^2 \\ g(x)=4x^2 \end{gathered}`

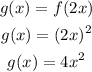
If x=0, so:

`g(0)=4*0^2=4*0=0`

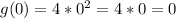
If x=1:

`g(1)=4*1^2=4*1=4`

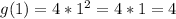
If x=-1:

`g(-1)=4*(-1)^2=4*1=4`

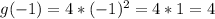
It means the function opens upward, and has its vertex at (0,0).

In the given graph, we can observe the x-axis and y-axis are divided every 2 units, then the first division at the right of the origin is equal to x=2. And the second division over the origin is equal to y=4.

Thus, we can observe in the second graph, that at x=1, the function takes the value y=4, and at x=-1, y=4 too, and the vertex of the graph is located at (0,0).

The answer is then option B.