1 Answer

Ask a Question

Ahmed Elkoussy · Answer 1 · 2023-07-27T16:36:03+0000

Use the ideal gas law for the initial and final conditions.

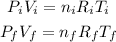
$\begin{gathered} P_iV_i=n_iR_iT_i \\ P_fV_f=n_fR_fT_f \end{gathered}$

Where P_i = 10^5 N/m^2, V_i = 400 m^3, T = 10 C = 283 K. So, we have the expression about the initial conditions

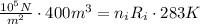
$(10^5N)/(m^2)\cdot400m^3=n_iR_i\cdot283K$

For the second expression, the final pressure and the final volume are the same because the hot-air balloon is open to the atmosphere.

$(10^5N)/(m^2)\cdot400m^3=n_fR_fT_f$

Then, use the density formula to find the initial mass and the final mass.

$\begin{gathered} m_i=\rho_iV=\frac{1.25\operatorname{kg}}{m^3}\cdot400m^3=500\operatorname{kg} \\ m_f=m_i-200\operatorname{kg}=500\operatorname{kg}-200\operatorname{kg}=300\operatorname{kg} \end{gathered}$

Now, we find the number of moles (n) by dividing the masses.

$(n_i)/(n_f)=\frac{500\operatorname{kg}}{300\operatorname{kg}}\approx1.67$

At last, we divide the initial equations (ideal gas law) to find the final temperature.

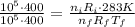
$(10^5\cdot400)/(10^5\cdot400)=(n_iR_i\cdot283K)/(n_fR_fT_f)$

The constant R is the same in both cases and use the ratio of moles.

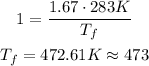
$\begin{gathered} 1=(1.67\cdot283K)/(T_f) \\ T_f=472.61K\approx473 \end{gathered}$

But, in Celsius, the temperature is 200 Celcius.

Therefore, the answer is D.

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions