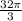First, notice that, by the Pythagorean Theorem,
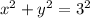
meaning that:
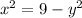
Also, since the volume of a cone with radius r and height h is
 we know that the volume of the cone is:
we know that the volume of the cone is:
![(1)/(3) \pi x^2 (3+y) = (1)/(3) \pi (9-y^2)(3+y) = (1)/(3) \pi [27+9y-3y^2-y^3]](https://img.qammunity.org/2016/formulas/mathematics/high-school/uic7i83hpakeyvifbkutih3vxytb7dc2ij.png)
Therefore, we want to maximize the function
![V(y) = (1)/(3) \pi [27+9y-3y^2-y^3]](https://img.qammunity.org/2016/formulas/mathematics/high-school/6p34foztg4bdpf2ewl4o1e6xu45b1dvv0s.png) subject to the constraint
subject to the constraint
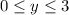 .
.
To find the critical points, we differentiate:
![V'(y)= (1)/(3) \pi [9-6y-3y^2] = \pi [3-2y-y^2] = \pi (3+y)(1-y).](https://img.qammunity.org/2016/formulas/mathematics/high-school/jkel3d7sw6kkeo995klw8d8zegbyql9iq7.png)
Therefore,
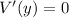 when
when
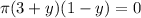
meaning that
 or
or
 . Only
. Only
 is in the interval
is in the interval
![[0,3]](https://img.qammunity.org/2016/formulas/mathematics/high-school/5ydlafh3dkbture2zd5ar9rb7tsbi4d9yf.png) so that’s the only critical point we need to concern ourselves with.
so that’s the only critical point we need to concern ourselves with.
Now we evaluate
 at the critical point and the endpoints:
at the critical point and the endpoints:
![V(0) = (1)/(3) \pi [27+9(0) - 3(0)^2] = 9 \pi](https://img.qammunity.org/2016/formulas/mathematics/high-school/or7y43oava4mcifg65uypu2350ccm1eosp.png)
![V(1) = (1)/(3) \pi [27+9(1)-3(1)^2-1^3] = (32 \pi )/(3)](https://img.qammunity.org/2016/formulas/mathematics/high-school/kznn3p1mq8onuwssjgtnibeq2t1sxy40g9.png)
![V(3) = (1)/(3) \pi [27+9(3) - 3(3)^2-3^2] = 0](https://img.qammunity.org/2016/formulas/mathematics/high-school/q7ktzvszav5mgd86vjp8hb68me35rtjhg4.png)
Therefore, the volume of the largest cone that can be inscribed in a sphere of radius 3 is