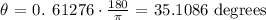Question

Your neighborhood movie theater has a 25-foot-high screen located 8 feetabove your eye level. If you sit too close to the screen, your viewing angle is toosmall, resulting in a distorted picture. By contrast if you sit too far back, theimage is quite small, diminishing the movie's visual impact. If you sit & feet backfrom the screen, your viewing angle is given by0 = tan-1 33-tan-11) Choose a value for ærepresenting how far back you want to sit in feet and usethe formula above to calculate the viewing angle 8 for that distance. Make sureyour calculator is in radian mode.2) Go to Movie Theater Mewing Angle and compare your choice of distance tothe optimal choice of distance. How close or far are you to the optimal(maximum) viewing angle?3) What is your viewing angle in degrees? (convert your angle to the nearesttenth)

Answer 1

1. We are given that the angle is determined by the formula

`\theta=tan^{\text{ - 1}}((33)/(x))-tan^{\text{ -1 }}((8)/(x))`

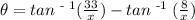
lets say we want to sit at x = 25 feet. So if we replace x with 25 and we plug it in our equation, using a calculator in radians we get

`\theta=tan^{\text{ -1}}((33)/(25))-tan^{\text{ -1}}((8)/(25))\text{ = }0.61276\text{ radians}`

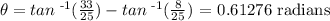
3. To transform one angle that is in radians, to degrees, we must mutiply by 180° and divide by pi radians. So, in our case we get

`\theta\text{ = 0. 61276}\cdot(180)/(\pi)\text{ = }35.1086\text{ degrees}`