The probability that a randomly chosen student scores 70 or below is 0.0013
Firstly, we want to calculate the z-score
We have this as;

Using this z-score, we proceed to calculate the probability as follows;
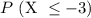
We use the standard normal distribution table for this
As we can see, this z-score value falls within 3 standard deviation from the mean
According to the empirical rule, the probability value here is 0.0013