Question

find how much money there will be in the account after the given number of years and find the interest earned round to the nearest hundred as needed for both

Answer 1

A principal $7000, rate 5%=0.05, and time 2 years is given.

It is stated that it is compounded semiannually, that is, twice in a year.

The question requires that you calculate the amount in the account after 2 years and the interest earned.

The formula for the amount (compound interest) is given as:

`A=P(1+(r)/(n))^(nt)`

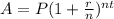
Where,

• A is the final amount.

,

• P is the principal

,

• r is the rate

,

• n is the number of times interest is compounded annually.

,

• t is the time in years.

In this case P=7000, r=0.05, n=2, t=2. Substitute these values into the formula:

`\begin{gathered} A=7000(1+(0.05)/(2))^(2(2))=7000(1+0.025)^4 \\ =7000(1.025)^4\approx7000(1.103813) \\ \approx\$7,726.69 \end{gathered}`

The equation that relates the amount, A, principal, P, and interest earned, I is given as:

`A=P+I`

Substitute A=7,726.69, P=7000 into the formula:

`\begin{gathered} 7,726.69=7,000+I \\ \Rightarrow I=7,726.69-7,000=\$726.69 \end{gathered}`

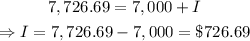
It follows that:

The amount of money in the account after 2 years is about $7,726.69.

The amount of interest earned is about $726.69.