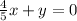The equation of a line in standard form is written as:
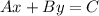
Now, two lines are parallel if and only if their slopes are equal, that is:
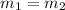
The slope of a line is given by:
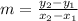
where (x1,y1) and (x2,y2) are points through the line. From the graph we notice that the line passes through the points (0,3) and (5,-1) then its slope is:
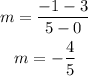
This means that the lin in the graph has a slope os -4/5 and hence the paralell line we are looking for has slope -4/5 as well.
Once we know the slope of the line we want we just need a point; the porblem states that the line passes through the origin, then it passes through the point (0,0). The equation of a line with slope m that passes throught the point (x1,y1) is given by:
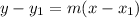
Plugging the values of the slope and the point we have that:
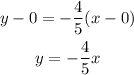
Finally we just write the equation in standard form, therefore the equation of the line is: