Question

The pilot of an airplane wishes to fly due north but there is 65km/h wind blowing toward the east. (a) In what direction should the pilot head her plane if it's speed relative to the air is 340km/h. (b) draw a vector diagram that illustrates your results in part a. (c) if the the pilot decreases the air speed of the plane but still wants to head due north should the angle found in part (a) be increased or decreased

Answer 1

(a) 11.02° west of north

(b) see diagram in EXPLANATION

(c) increased

Step-by-step explanation

(a) The pilot wants the airplane to fly north. There's a speed relative to the air that is 340km/h and the air speed is 65km/s. Drawing a vector diagram (b) we can see how to find the direction the plane should head:

If the wind is blowing east, it is clear that the plane has to go in opposite direction but still heading north. So the direction is θ degrees west of north. Now we just have to find this angle. The vectors form a right triangle where the direction the angle should take is the hypotenuse and the direction of the wind is the opposite side to the angle θ. Using the sine of the angle:

`\sin \theta=(13)/(68)`

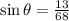
Solving for θ:

`\theta=\sin ^(-1)(13)/(68)=11.02\degree`

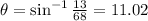
(c) Let's draw a new diagram with a smaller red vector:

If the red vector (which represents the speed of the plane) is exaggeratedly smaller than before we can see graphically that the angle is increased if the speed of wind's vector is the same.