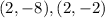Question

Which conic section does the equation below describe? (x - 9) + (+2) . v = 1 4 25 O A. Parabola O B. Circle O c. Ellipse O D. Hyperbola

Answer 1

The vertices of the ellipse are:

`(2,-8),(2,-2)`

SOLUTION

Problem Statement

The question gives us the equation of an ellipse. We are asked to find the coordinate of the vertices of the major axis.

Method

The equation of the ellipse given is:

`((x-2)^2)/(4)+((y+5)^2)/(9)=1`

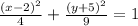
The major axis of the ellipse is the term with the larger denominator. The larger denominator is 9, thus the y-axis is the major axis.

This thus implies that the coordinates we are most interested in are the topmost and bottom vertices of the ellipse.

To find the coordinates of this axis, we just need to know the formula stated below:

`\begin{gathered} \text{Given the equation of an ellipse:} \\ ((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1 \\ where, \\ (h,k)\text{ is the center of the ellipse} \\ a,b\text{ represent the minor and major axes.} \\ \\ \text{Topmost point = }(h,k+b) \\ \text{Bottom most point }=(h,k-b) \end{gathered}`

Using the formula for the Topmost point and the Bottom most point, above, we would find the coordinate of the vertices of the ellipse

Implementation

`\begin{gathered} \text{Comparing the equation of the ellipse given to the general formula in the Method section:} \\ h=2,k=-5 \\ a^2=4,a=\pm2 \\ b^2=9,b=\pm3 \\ \\ \text{Topmost point }=(h=2,k+b=-5+-3)=(2,-8) \\ \text{Bottom most point}=(h=2,k-b=-5-(-3))=(2,-2) \end{gathered}`

Final Answer

Therefore, the vertices of the ellipse are:

`(2,-8),(2,-2)`