Question

Consider the equation: 32 + 10.0 +9 = 0 A) First, use the "completing the square" process to write this equation in the form (x + D) enter your results below. = E and z? + 10x + 9 = 0 is equivalent to: = Preview left side of egn: B) Solve your equation and enter your answers below as a list of numbers, separated with a comma where necessary. Answer(s):

Answer 1

A) Given the quadratic expression:

`x^2+10x+9=0`

First, identify the coefficients of the expression:

a is the coefficient of the quadratic term, in this case, a=1

b is the coefficient of the x-term, in this case, b=10

Second, divide all terms by a=1, since we are dividing by one and the expression will remain the same, you can skip this step.

Third, pass the constant to the right side of the equation by applying the opposite operation to both sides of it:

`\begin{gathered} x^2+10x+9-9=0-9 \\ x^2+10x=-9 \end{gathered}`

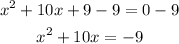
Forth, complete the square by adding (b/2)²

For this expression b=10 so that:

`((b)/(2))^2=((10)/(2))^2=5^2^{}=25`

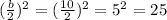
So you have to add 25 to both sides of the expression:

`\begin{gathered} x^2+10x+25=-9+25 \\ x^2+10x+25=16 \end{gathered}`

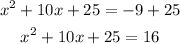
The simplified expression is:

`(x+5)^2=16`

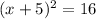
B)

To solve the expression you have to take the square root to both sides of it:

`\begin{gathered} \sqrt[]{(x+5)^2}=\sqrt[]{16} \\ x+5=\pm4 \end{gathered}`

To determine the possible values of x, you have to solve both options separatelly:

1)