Question

Could an even or an odd function be transformed into the other (even to odd or odd to even)? Why or why not? Give an example.

Answer 1

The even and odd functions are functions that satisfy particular symmetry operations with repcet to taking additive inverses. A function,

`f(x)=x^n`

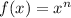
is said to be, even, if n is an even integer and odd function when n is an odd integer.

Also, for a function if,

`\begin{gathered} f(x)=f(-x)\rightarrow even \\ -f(x)=f(-x)\rightarrow odd \end{gathered}`

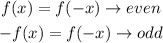
An even or an odd function be transformed into the other.

The product of two odd functions is an even function.

The product of an even function and an odd function is an odd function.

The quotient of two odd functions is an even function.