Question

Ind the solution of the system of equations. - 9x – 5y = -18 4x + 5y = 33 Submit Answer

Answer 1

We are given the following system of equations:

`\begin{gathered} -9x-5y=-18,\text{ (1)} \\ 4x+5y=33,\text{ (2)} \end{gathered}`

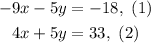
We are asked to solve the system, to do that we can solve for "y" in equation (1), and replace that value in equation (2), like this.

`-9x-5y=-18`

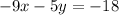
adding 9x on both sides

`\begin{gathered} -9x+9x-5y=-18+9x \\ -5y=-18+9x \end{gathered}`

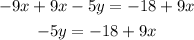
dividing by -5 on both sides:

`y=(-18+9x)/(-5)`

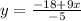
replacing this value of "y" in equation (2) we get:

`\begin{gathered} 4x+5y=33 \\ 4x+5((-18+9x)/(-5))=33 \end{gathered}`

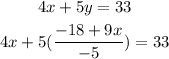
Simplifying we get:

`4x+18-9x=33`

adding like terms:

`-5x+18=33`

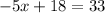
subtracting 18 on both sides

`\begin{gathered} -5x+18-18=33-18 \\ -5x=15 \end{gathered}`

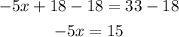
dividing by -5 on both sides:

`x=(15)/(-5)=-3`

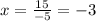
Now we can find the value of "y" replacing the value of "x" that we have found, like this:

`y=(-18+9x)/(-5)`
`y=(-18+9(-3))/(-5)`

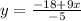
Solving the operations:

`y=(-18-27)/(-5)=(-45)/(-5)=9`

Therefore, the solution of the system is x = -3 and y = 9