Question

Need the answers quick for 3a , b, and c

Answer 1

3a)

Set g(x)=f'(x); then, g'(x)=f''(x).

Notice that in the limit when approaching x=2 in the graph of g(x), g(x) has a 'sharp' minimum (like in the case of the absolute value function), and the derivative cannot be defined in such situations.

One cannot find the value of f''(2) because the function f''(x) is not defined on that value of x. Therefore, we say that the function is not smooth on x=2.

3b)

According to the graph, f(x) has 4 critical points in the interval.

Notice that, in the case of a maximum

On the other hand, in the case of a minimum.

This means that the values of the slopes of the tangent lines to f(x) (the value of the derivative) are positive to the left of the maximum and negative to the right of it.

Therefore, in our case,

To the left of x=-2, f'(x)<0; and to the right of x=-2, f'(x)>0->f(-2) is a minimum

To the left of x=2, f'(x)>0; and to the right of x=2, f'(x)>0->f(2) is neither a minumum nor a maximum

To the left of x=6, f'(x)>0; and to the right of x=-2, f'(x)<0->f(6) is a maximum.

To the left of x=10, f'(x)<0; and to the right of x=2, f'(x)<0->f(10) is neither a minumum nor a maximum.

In a drawing, f(2) and f(10) look like this.

The only maximum is at f(6).

3c)

`\begin{gathered} g(x)=x^3f(x) \\ \Rightarrow g^(\prime)(x)=(x^3f(x))^(\prime)=(x^3)^(\prime)f(x)+x^3f^(\prime)(x) \\ \Rightarrow g^(\prime)(x)=3x^2f(x)+x^3f^(\prime)(x) \end{gathered}`

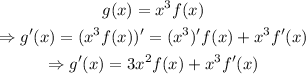
Thus,

`\begin{gathered} \Rightarrow g^(\prime)(1)=3(1)^2f(1)+(1^{})^3f^(\prime)(1)=3f(1)+f^(\prime)(1)=3\cdot7+2=23 \\ \Rightarrow g^(\prime)(1)=23 \end{gathered}`

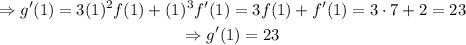
The answer is g'(1)=23