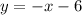Question

Write the slope intercept of the equation of the line through the given points. Through (-2,-4) and (-3,-5)

Answer 1

The slope between two(2) points;

`\begin{gathered} P(x_1,y_1)_{} \\ \text{and Q(x}_2,y_2) \end{gathered}`

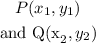
is given as:

`m=(y_2-y_1)/(x_2-x_1)`

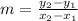
From the question, the given points are:

`\begin{gathered} (-2,-4)\text{ and (-3,-5)} \\ \Rightarrow x_1=-2,y_1=-4 \\ \Rightarrow x_2=-3,y_2=-5 \end{gathered}`

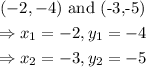
Thus, the slope, m, is:

`\begin{gathered} m=(-5-(-4))/(-3-(-2)) \\ m=(-5+4)/(-3+2) \\ m=(-1)/(-1) \\ m=-1 \end{gathered}`

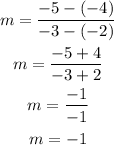
The equation of a line with two(2) given points is given as:

`m=(y-y_1)/(x-x_1)`

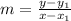
Thus,

`\begin{gathered} -1=(y-(-4))/(x-(-2)) \\ -1=(y+4)/(x+2) \\ \text{cross}-\text{multiply} \\ y+4=-1(x+2) \\ y+4=-x-2 \\ y=-x-2-4 \\ y=-x-6 \end{gathered}`

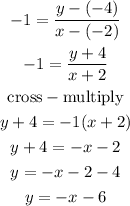
Hence, the slope-intercept form of the equation of the line through the given points is:

`y=-x-6`