1 Answer

Ask a Question

Alalonde · Answer 1 · 2023-01-07T04:36:11+0000

Part 1

To find the range, we subtract the lowest value from the greatest value, ignoring the others.

So, in this case, we have:

• Lowest value: 20.3

,

• Greatest value: 110.4

$\text{Range = }110.4-20.3=90.1$

Therefore, the range is 90.1

Part 2

The formula to find the variance is

$\begin{gathered} \sigma^2=\frac{\sum ^{}_{}(x-\mu)^2}{n} \\ \text{ Where} \\ x=\text{ data values} \\ \mu=\text{ mean} \\ n=\text{ number of data points} \end{gathered}$

The formula to find the mean is

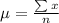
$\mu=\frac{\sum ^{}_{}x}{n}$

So, as you can see, we first find the mean, and with this value, we find the variance of the data set.

• Mean

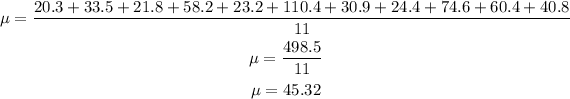
$\begin{gathered} \mu=(20.3+33.5+21.8+58.2+23.2+110.4+30.9+24.4+74.6+60.4+40.8)/(11) \\ \mu=(498.5)/(11) \\ \mu=45.32 \end{gathered}$

• Variance

$\begin{gathered} \sigma=((20.3-45.32)^2+(33.5-45.32)^2+(21.8-45.32)^2+(58.2-45.32)^2+(23.2-45.32)^2+(110.4-45.32)^2+(30.9-45.32)^2+(24.4-45.32)^2+(74.6-45.32)^2+(60.4-45.32)^2+(40.8-45.32)^2)/(11) \\ \sigma=((-25.02)^2+(-11.82)^2+(-23.52)^2+(12.88)^2+(-22.12)^2+(65.08)^2+(-12.42)^2+(-20.92)^2+(29.28)^2+(15.08)^2+(-4.52)^2)/(11) \\ \sigma=(625.91+139.67+553.10+165.94+489.21+4325.64+207.88+437.57+857.42+227.46+20.41)/(11) \\ \sigma=(7960.24)/(11) \\ $$\boldsymbol{\sigma=723.66}$$ \end{gathered}$

Therefore, the variance is 723.66.

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions