SOLUTION
The function given is
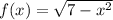
The domain of a function is the set of input values (x-values) for which the function is defined or real.
To obtain the domain of the function above, we need to solve the expression in the square root.
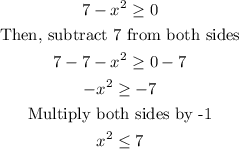
Take square root of both sides we have
![\begin{gathered} √(x^2)\le\pm\sqrt[]{7} \\ \text{Then} \\ x^{}\le\pm\sqrt[]{7} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5um1xcc3wzn19u7w916f.png)
Hence, the domain becomes
![\begin{gathered} -√(7)\le\: x\le√(7) \\ or \\ \mleft[-√(7),\: √(7)\mright] \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/m4kf42auvar9ygcmlux3.png)
Domain is [-√7,√7]
Similarly, for th range of f(x) we have
![\begin{gathered} \mleft[0,\: √(7)\mright] \\ or \\ \: 0\le\: f\mleft(x\mright)\le√(7) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/jrxjdvcsa5yfmfzf4v2e.png)
Therefore
Range is [0,√7]