In order to determine the height at which the package can be dropped, use the following formula:
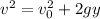
where,
v: final speed = 55.0mph
g: gravitational acceleration constant = 9.8 m/s^2
y: height = ?
vo: inital speed of the package = 0 m/s
Convert mph to m/s first:
![55\text{mph}\cdot\frac{1.6\operatorname{km}}{1\text{mile}}\cdot\frac{1000m}{1\operatorname{km}}\cdot(1h)/(3600s)=(24.44m)/(s)]()
Next, solve the equation above for y and replace the values of the other parameters:

Hence, at 30.48m the package reaches the ground with the critical speed.
Moreover, for 20m the package be safely dropped.