.We have the following equation,
![\sqrt[]{7-x}=x+5](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/nvdlekgg425voy2jlvw8.png)
First, we can note that the term into the radical must be zero or positive, that is,
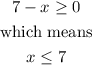
Then, by squaring both sides, we have

Now, by subtracting 7 to both sides, we have
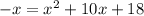
and by adding x to both sides, we get
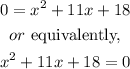
Now, we can use the quadratic formula, that is,
![x=\frac{-11\pm\sqrt[]{11^2-4(1)(18)}}{2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/blg407w27ek289grqyg8.png)
which gives
![\begin{gathered} x=\frac{-11\pm\sqrt[]{121-72}}{2} \\ x=\frac{-11\pm\sqrt[]{49}}{2} \\ x=(-11\pm7)/(2) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ytd1bwycbna9jsu11eo1.png)
then, the solutions are
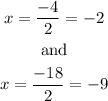
Now, we know that an extraneous solution is a solution that does not work. Then, by substituting x=-9 into the given equation, we have
![\sqrt[]{7-(-9)}=-9+5](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/iy91225zuxkanou2x2ye.png)
which gives
![\begin{gathered} \sqrt[]{7+9}=-4 \\ \sqrt[]{16}=-4 \\ 4=-4 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/3h6ld8jh38legjo95sw9.png)
which is an absurd result. Then, x=-9 is an extraneous solution.
On the other hand, by substituting x=-2, we obtain
![\begin{gathered} \sqrt[]{7-(-2)}=-2+5 \\ \sqrt[]{7+2}=3 \\ \sqrt[]{9}=3 \\ 3=3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ii1yhv90iqp600o4hhd5.png)
which is correct.
Therefore, the answers are:
