Question

Which equation describes the circle having center point (4,2) and radius r = 3 in standard form? O A. (x-4)² + (y-2)² = 3 O B. (x+4)² + (x + 2)² = 9 Oc. (x+4)2 + (+ 2)2 =3 O D. (x-4)² + (x - 2)² =9

Answer 1

The correct option is

D. (x-4)^2 + (y-2)^2 = 9

The equation of a circle that has center in a point P = (h, k) is:

`(x-h)^2+(y-2)^2=r^2`

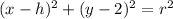
Where r is the radius. In this case the center is in (4, 2). Then we can rplace h and k:

`(x-4)^2+(y-2)^2=r^2`

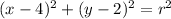
All that is left is replace r by the radius. In this case r = 3 then r^2 = 9

Now we can complete the equation:

`(x-4)^2+(y-2)^2=9`

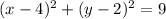
And that's option D.