Question

A plane flies 620km [S 30° W] then 290km [N 25° W]. Determine the displacement of theplane.

Answer 1

To help us solve the problem we draw each displacement given in the problem as a vector on the plane:

Now, we know that the components of a vector are given by:

`\begin{gathered} u_x=u\cos\theta \\ u_y=u\sin\theta \\ \text{ where} \\ u\text{ is the magnitude of the vector } \\ \theta\text{ is the angle of the vector measure from the x-axis counterclockwise} \end{gathered}`

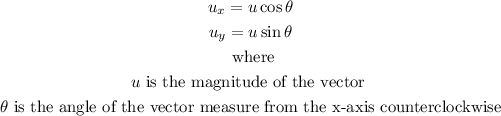
For the 620 km displacement, we know that its magnitude is 620 km and its angle is 240° (with respect to the x-axis in the direction stated above), then we have:

`\vec{r}_1=620\cos240\hat{i}+620\sin240\hat{j}`

For the 290 km the displacement, we know that its magnitude is 290 km and its angle is 115°, then we have:

`\vec{r}_2=290\cos115\hat{i}+290\sin115\hat{j}`

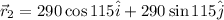
Now, the total displacement of the plane is the sum of this two vectors then we have:

`\begin{gathered} \vec{r}=\vec{r}_1+\vec{r}_2 \\ =(620\cos240\hat{i}+620\sin240\hat{j})+(290\cos115\hat{i}+290\sin115\hat{j}) \\ =(620\cos240+290\cos115)\hat{i}+(620\sin240+290\sin115)\hat{j} \\ =-432.56\hat{i}-274.11\hat{j} \end{gathered}`

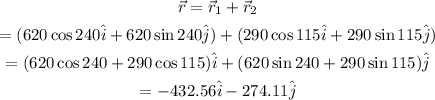
Hence, the displacement of the plane is:

`\vec{r}=-432.56\hat{i}-274.11\hat{j}`

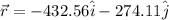
Finally we get the magnitude of the vector:

`\begin{gathered} r=√((-432.56)^2+(-274.11)^2) \\ r=512.1 \end{gathered}`

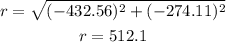
Therefore, the displacement of the plane is 512.1 km